（本貼文所列出的程式碼，皆以 colab 筆記本方式執行，[可由此下載]
(https://colab.research.google.com/drive/1mdQomdLzs2GZnu1tsNbRXLIr4X-ggNkx?usp=sharing)

自動向量化簡介

起初在研讀 JAX 的時候看到它談論到「自動向量化 Automatic Vectorization」，這個在平行運算 (parallel computing) 和編譯器 (compiler) 領域中的概念，和 JAX 及機器學習會有什麼關係？

從平行運算的觀點來看

要摸清其中的來龍去脈，需先從傳統上我們知道的自動向量化談起。維基百科關於它的定義是 [28.1]：

Automatic vectorization, in parallel computing, is a special case of automatic parallelization, where a computer program is converted from a scalar implementation, which processes a single pair of operands at a time, to a vector implementation, which processes one operation on multiple pairs of operands at once.

在平行運算的領域裏，自動向量化乃是「自動平行化」技術中的一個特例，它將程式中兩程純量間的運算，自動轉換為兩個向量間的運算。(按：這段是老頭自己的翻譯。)

舉個 C 語言的例子，考慮以下的片斷：

n = 16;
int a[16];
int b[16];
int c[16];

…
… // 初始化 a, b 陣列的值
…

for (i=0; i < n; i++)
	c[i] = a[i] + b[i];
…

如果不做向量化的動作，這段程式執行時，會依序的執行 16 次下面的動作：

step 1: 把陣列 a 的一個元素放入暫存器，
step 2: 把陣列 b 的一個元素放入另一個暫存器，
step 3: 執行純量加法，
step 4: 把結果存入 c 的相對應位置。

如果在支援向量運算的硬體上，執行自動向量化的動作，那麼上述的 C 程式可能就可以被編譯成：

step 1: 把陣列 a 整個放入向量暫存器，
step 2: 把陣列 b 整個放入另一個向量暫存器，
step 3: 執行向量加法，
step 4: 把結果存入 c 。

一般來講，向量運算的速度，當然會比其對等的純量運算的速度要快得多了！

從機器學習的觀點來看

從機器學習的觀點，自動向量化其實就是我們熟悉的「批次 batch」概念。在訓練模型的時候，我們不再把訓練資料一個一個的輸入模型，不再針對每一個別的訓練資料來調整模型參數（當然，在某些特殊的情況下，我們仍然會這麼做），而是把個別訓練資料，重組成更大的資料陣列，稱之為批次，模型訓練時，一個批次一個批次的將其輸入模型，每一個批次調整一次模型參數。

假設我們有 10000 張照片用來訓練一個分類模型，我們可以將每 10 張照片組成一個批次，共成為 1000 個批次的訓練資料，每一個回合 (cycle) 的訓練，我們分別將 1000 個批次依序輸入模型，並調整參數 1000 次。這樣，可以讓模型訓練的速度更快，更有效率。

當然在模型推理的時候，也可以利用批次的概念，一次處理多個輸入資料。

JAX 提供了 jax.vmap() API 讓我們很容易的實現批次訓練及推理！

老頭曾經想過，為什麼 JAX 不用像是 batching 這樣的字眼來描述 vmap 而要用 Automaitc Vectorization？它的原因可能是 JAX 不單單只是應用在機器學習，它也適合於跟線性代數有關的其他研究領域，對於他們而言，Automatic Vectorization 可能遠比 batching 來得容易理解。

vmap 的用法

我們現在就用一個簡單的卷積 (convolve) 運算函式來說明 vmap 的用法。

先定義這個卷積函式，它的輸入參數 x 是一個一維陣列，並假定它的長度不小於 3 ，它的另一個參數 w 是卷積的內核 (kernel) ，其 shape 為 (3, 0)。

# assume x : rank = 1
# assume w : shape = (3,)
 
def convolve(x,w):    
    output = []
    for i in range(1, len(x)-1):
        output.append(jnp.dot(x[i-1:i+2], w))
        
    return jnp.array(output)

接下來準備我們要測試的資料，x 是我們的訓練資料，共有六筆 (x0 至 x5) ，w 是內核，初值設為 [1., 1., 1.]。

# define the data
 
# 訓練資料
x0 = jnp.arange(0,10)
x1 = jnp.arange(10,20)
x2 = jnp.arange(20,30)
x3 = jnp.arange(30,40)
x4 = jnp.arange(40,50)
x5 = jnp.arange(50,60)
 
# 內核
w = jnp.array([1., 1., 1.])

接下來把訓練資料集組合為一個高維度的「訓練資料集 dataset」陣列，我們先沿第一個維度排列資料，再做一個沿最後維度排列的資料集。

# define dataset
 
Xs_1st_axis = jnp.array([x0,x1,x2,x3,x4,x5])
Xs_last_axis = Xs_1st_axis.swapaxes(0,1)

單一資料處理

準備工作都完成了，現在可以開始做實驗。因為我們設計 convolve () 函式的時候，是以處理單獨一筆訓練資料來設計的，因此，正常使用時，要一筆一筆的分別輸入，得到一筆一筆分別的結果。不同維度排列的資料集，得到的結果是一致的。

# process single data a call : 第一維度
 
for x in Xs_1st_axis:
    print(convolve(x,w))

output:
[ 3. 6. 9. 12. 15. 18. 21. 24.]
[33. 36. 39. 42. 45. 48. 51. 54.]
[63. 66. 69. 72. 75. 78. 81. 84.]
[ 93. 96. 99. 102. 105. 108. 111. 114.]
[123. 126. 129. 132. 135. 138. 141. 144.]
[153. 156. 159. 162. 165. 168. 171. 174.]

# process single data a call : 最後維度
 
for idx in range(Xs_last_axis.shape[-1]):
    x = Xs_last_axis[:,idx]
    print(convolve(x,w))

output:
[ 3. 6. 9. 12. 15. 18. 21. 24.]
[33. 36. 39. 42. 45. 48. 51. 54.]
[63. 66. 69. 72. 75. 78. 81. 84.]
[ 93. 96. 99. 102. 105. 108. 111. 114.]
[123. 126. 129. 132. 135. 138. 141. 144.]
[153. 156. 159. 162. 165. 168. 171. 174.]

批次處理 :

如果我們想要對 Xs_1st_axis (沿第一維度排列) 這個資料集做批次處理，又不想要重寫 convolve 函式的話，要怎麼辦呢？jax.vmap() 要上場了：

# define the vmap funcion : 1st axis
vmap_convolve_1st = jax.vmap(convolve, in_axes=(0,None))
 
vmap_convolve_1st(Xs_1st_axis, w)

output:

我們使用 jax.map() 轉換 convolve 函式，並且利用 in_axes= 參數來指定我們的資料批次的方式。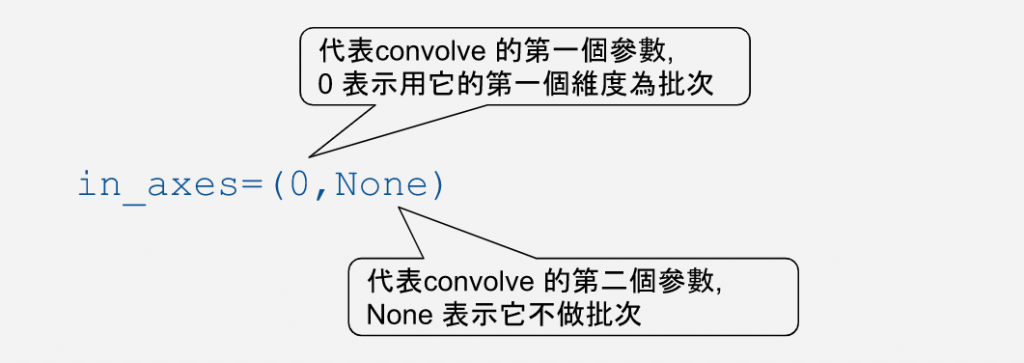

將批次資料輸入轉換過的函式 vmap_convolve_1st() ，我們可以看到，它的結果和之前一個一個輸入的方式是一致的。

同樣的，我們也可以用最後一個維度排列的資料集 Xs_last_axis 作為輸入，其程式段如下：

# define the vmap funcion : last axis
vmap_convolve_last = jax.vmap(convolve, in_axes=(-1,None))
 
vmap_convolve_last(Xs_last_axis, w)

output:

執行效率的比較

又到了令人振奮的 PK 時間！

先確認執行環境。老頭是在 colab 上，一個 GPU 的環境下：

# to check current environment
jax.devices()

output:
[GpuDevice(id=0, process_index=0)]

分別量測時間：

def f():
    for x in Xs_1st_axis:
        convolve(x,w)
 
%timeit f()        

output:
26.9 ms ± 584 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit vmap_convolve_1st(Xs_1st_axis, w)

output:
13.7 ms ± 229 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit jax.jit(vmap_convolve_1st)(Xs_1st_axis, w).block_until_ready()

output:
378 µs ± 8.01 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

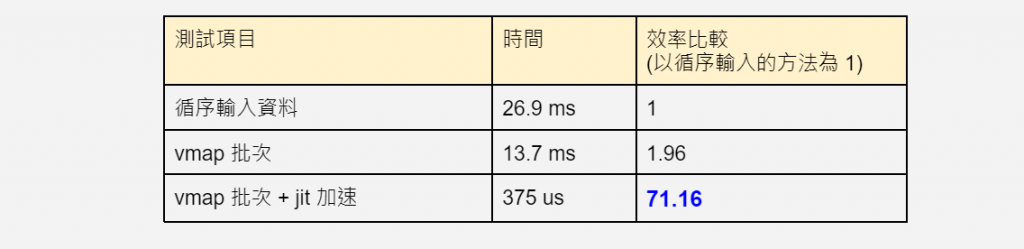
vmap + jit 的威力，從這個比較當中，一覽無遺，超過 70 倍的效率提升！

註：

[28.1] 目前維基百科上只有英文版本的定義。